Reading the original code of the KAN: Kolmogorov-Arnold Networks paper was a bit confusing for me so I tried to implement a simple KAN from scratch. You can find the original code on pykan repo.
The code written in this post is hosted here.
This post is unfinished. Will be completed. { : .prompt-info }
B-spline Curves
Theory
reference: B-splines curves and surfaces
Basis Functions
Basis functions are basic building blocks of all the functions in a function space. Every function in the function space can be represented as a linear combination of its basis functions.
Think of exponentials that are basis functions of any periodic function that has a fourier series.
Spline
A spline is a piecewise polynomial function \(S: [a, b] \rightarrow \mathbb{R}\) with \(m+1\) knots \(t = [t_0, ..., t_m]\) where \(a=t_0\le t_1 \le ... \le t_m=b\) and:
\[S(x) = P_i(x), \qquad x\in[t_i, t_{i+1})\]for \(i=0,..,m-1\).
If the polynomial pieces \(P_i\) each have degree at most \(p\), then the spline is said to be of degree \(p\) or of order \(p+1\).
B-spline
A B-spline (basis spline) of order \(p+1\) is a piecewise polynomial function \(B_{i, k}(x)\) of degree \(p\). B-splines are basis functions for spline functions of the same order and are defined as:
\[B_{i, 0}(x) = 1,\qquad if~x\in[t_i,t_{i+1}),~o.w.~0\]and recursively:
\[B_{i, p}(x) = \frac{x - t_i}{t_{i+p}-t_i}B_{i, p-1}(x) + \frac{t_{i+p+1} - x}{t_{i+p+1}-t_{i+1}}B_{i+1, p-1}(x)\]for \(p > 0\), and \(i=0,...,n-1\), and \(t = [t_0, ..., t_{n+p}]\).
B-spline Curve
A B-spline curve is defined as a linear combination of B-spline basis functions with the knot vector \(t = [t_0,..,t_p,..,t_n,..t_{n+p}]\):
\[S(x) = \sum_{i=0}^{n - 1} c_i B_{i, p}(x), \qquad x\in[t_{p}, t_{n}]: \text{internal knots}\]with \(n > p\).
Implementation
1
2
import numpy as np
from matplotlib import pyplot as plt
Scaler
1
2
3
4
5
6
7
8
9
10
11
def b(x, i, p, t):
if p == 0:
return 1 if t[i] <= x < t[i + 1] else 0
c_1 = (x - t[i]) / (t[i + p] - t[i])
c_2 = (t[i + p + 1] - x) / (t[i + p + 1] - t[i + 1])
b_ip = c_1 * b(x, i, p - 1, t) + c_2 * b(x, i + 1, p - 1, t)
return b_ip
def b_curve(x, c, p, t):
return sum([ci * b(x, i, p, t) for i, ci in enumerate(c)])
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
p = 3 # dgree of polynomials
n = 6 # number of basis functions (> p)
m = n + p + 1 # number of knots
t = np.linspace(0, 1, m) # uniform knot vector (t[p:n+1] are called internal knots)
x = np.linspace(t[0], t[-1], 100)
fig, ax = plt.subplots(figsize=(16, 4))
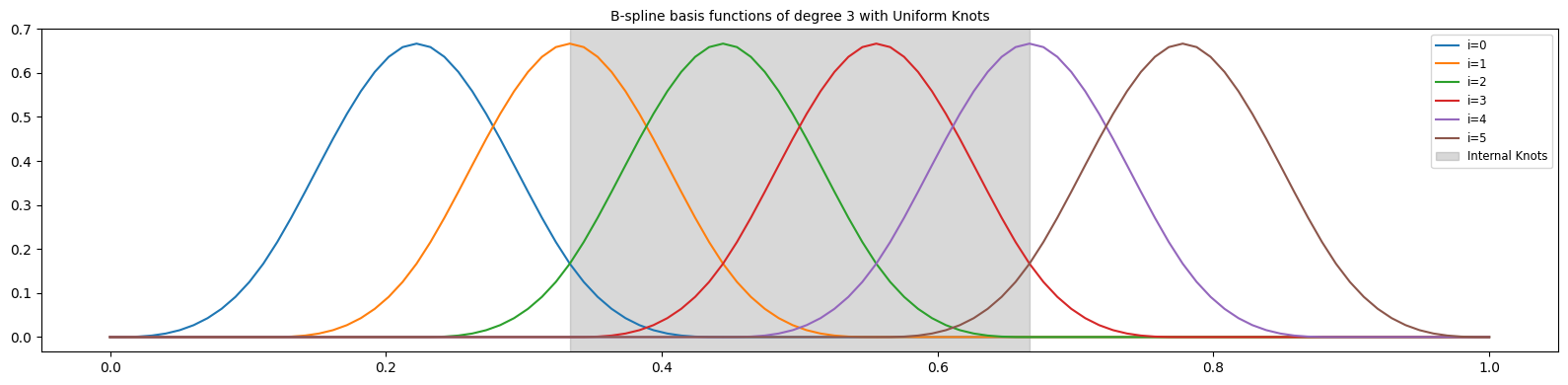
for i in range(n):
y = [b(xi, i, p, t) for xi in x]
ax.plot(x, y, label=f"i={i}")
ax.axvspan(t[p], t[n], color="gray", alpha=0.3, label="Internal Knots")
ax.set_title(
"B-spline basis functions of degree 3 with Uniform Knots", fontsize="medium"
)
ax.legend(fontsize="small")
fig.tight_layout()
1
2
3
4
5
6
7
8
9
10
fig, ax = plt.subplots(4, 4, figsize=(12, 12), sharex=True, sharey=True)
ax = ax.flatten()
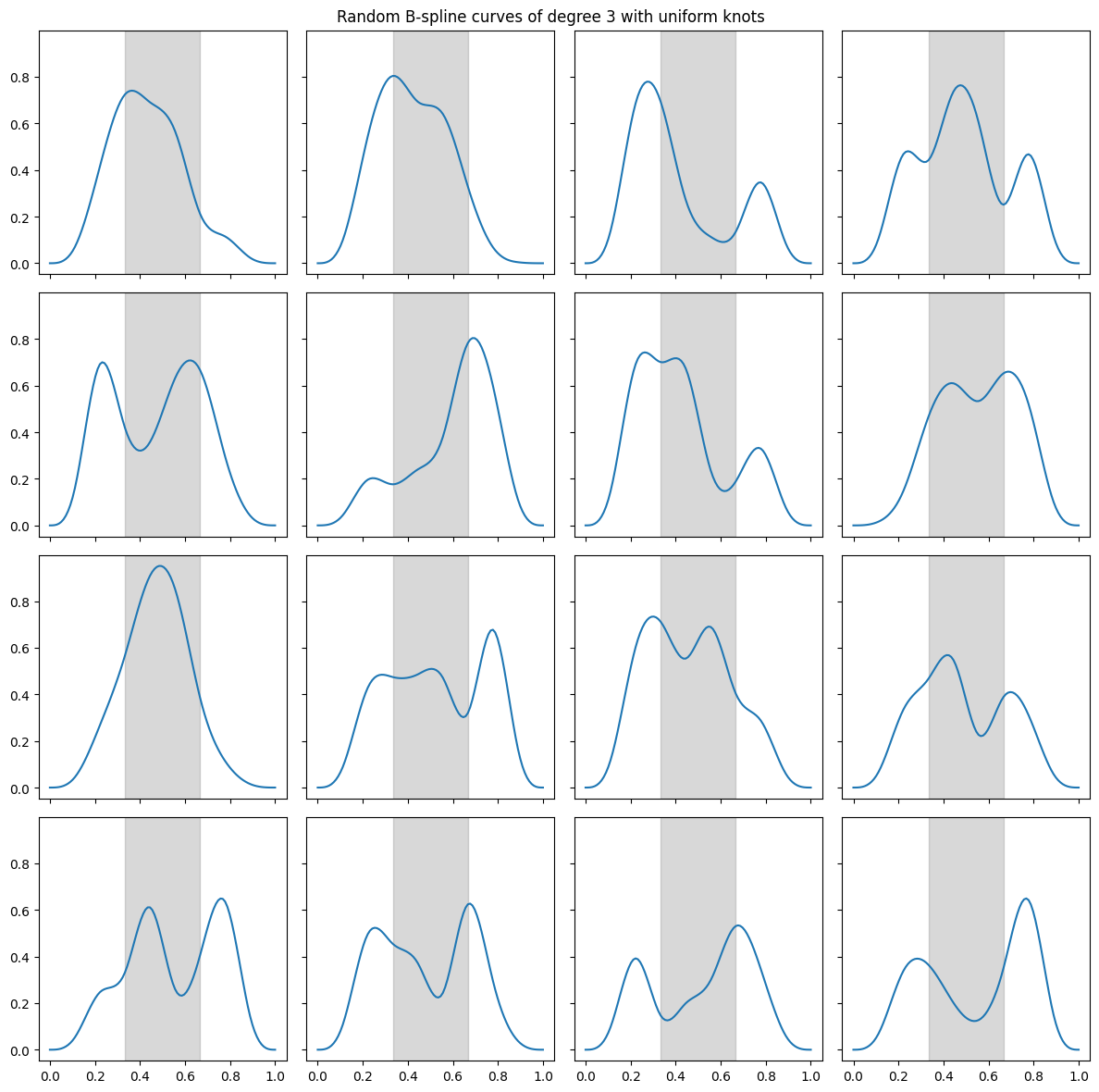
for i in range(16):
c = np.random.random(n)
y = [b_curve(xi, c, p, t) for xi in x]
ax[i].plot(x, y)
ax[i].axvspan(t[p], t[n], color="gray", alpha=0.3)
fig.suptitle("Random B-spline curves of degree 3 with uniform knots")
fig.tight_layout()
Batch
If x is a batch of shape $(N, d)$, with simple modification we can have the batched version of the basis functions.
1
2
3
4
5
6
7
8
def b_batch(x, i, p, t):
if p == 0:
out = (t[i] <= x) * (x < t[i + 1])
return out.astype(int)
c_1 = (x - t[i]) / (t[i + p] - t[i])
c_2 = (t[i + p + 1] - x) / (t[i + p + 1] - t[i + 1])
b_ip = c_1 * b_batch(x, i, p - 1, t) + c_2 * b_batch(x, i + 1, p - 1, t)
return b_ip
Batch for all bases
1
2
3
4
5
6
7
8
9
10
11
12
13
14
# For all i = 0, ..., n-1
def b_vectorized(x, p, t):
m = t.shape[0]
n = m - p - 1
t = t.reshape(-1, 1, 1)
if p == 0:
out = (t[:-1] <= x) * (x < t[1:])
return out.astype(int)
c_1 = (x - t[:n]) / (t[p : p + n] - t[:n])
c_2 = (t[p + 1 : n + p + 1] - x) / (t[p + 1 : n + p + 1] - t[1 : n + 1])
b_pm1 = b_vectorized(x, p - 1, t)
b_p = c_1 * b_pm1[:-1] + c_2 * b_pm1[1:]
return b_p
1
2
3
4
5
6
7
8
9
p = 3 # dgree
n = 6 # number of basis functions (> p)
m = n + p + 1 # number of knots
N = 16 # batch size
d = 8 #
t = np.linspace(0, 1, m) # uniform knot vector (t[p:n+1] are called internal knots)
x = np.random.random((N, d))
B = b_vectorized(x, p, t)
B.shape
1
(6, 16, 8)
Batch for all bases with different knot vectors
1
2
3
4
5
6
7
8
9
10
11
12
13
def b_vectorized(x, p, t):
m, d = t.shape
n = m - p - 1
t_ = t.reshape(m, 1, d)
if p == 0:
out = (t_[:-1] <= x) * (x < t_[1:])
return out.astype(int)
c_1 = (x - t_[:n]) / (t_[p : p + n] - t_[:n])
c_2 = (t_[p + 1 : n + p + 1] - x) / (t_[p + 1 : n + p + 1] - t_[1 : n + 1])
b_pm1 = b_vectorized(x, p - 1, t)
b_p = c_1 * b_pm1[:-1] + c_2 * b_pm1[1:]
return b_p
1
2
3
4
5
6
7
8
9
10
11
p = 3 # dgree
n = 6 # number of basis functions (> p)
m = n + p + 1 # number of knots
N = 16 # batch size
d = 8 #
t = np.sort(
np.random.random((m, d)), axis=1
) # uniform knot vector (t[p:n+1] are called internal knots)
x = np.random.random((N, d))
B = b_vectorized(x, p, t)
B.shape
1
(6, 16, 8)